kingdomvorti.blogg.se - Properties of isosceles triangles deltamath

The legs of the Golden triangle are in the golden ratio relative to the base. It has a vertex angle measuring 36° and base angles of 72°. The golden triangle is a special isosceles triangle that is also referred to as the sublime triangle. Since x in this case is 12, we find c by multiplying by : Side b = 12 because it has the same measure as the known side. This relationship allows us to find the missing lengths using simple algebra given the length of either the hypotenuse or one of the congruent sides.įind the lengths of the missing sides of the 45-45-90 triangle below. The sides of a 45-45-90 triangle have the following relationship: Isosceles acute triangleĪn isosceles acute triangle is a triangle with 2 congruent sides and angles in which all the angles are acute.Īn isosceles obtuse triangle is a triangle with 2 congruent sides and angles in which the non-congruent angle is obtuse.Īn isosceles right triangle is a triangle with 2 congruent sides and angles in which the non-congruent angle measures 90°.īecause the sum of a triangle's interior angles is equal to 180°, the remaining two angles in an isosceles right triangle measure 45° (90 + 45 + 45 = 180°).Ī 45-45-90 triangle is a special type of right triangle. Also, all equilateral triangles are also classified as isosceles since they have 3 congruent sides and angles. Isosceles triangles can further be categorized as acute, obtuse, and right. Generally, triangles are categorized as acute, obtuse, right, isosceles, scalene, and equilateral. There are a few different types of isosceles triangles. The altitude drawn from the vertex angle to the base divides an isosceles triangle into two congruent right triangles.Side opposite the vertex angle is the base.So, ∠B ≅ ∠C, since corresponding parts of congruent triangles are also congruent. Based on this, △ADB ≅ △ADC by the Side-Side-Side theorem for congruent triangles since BD ≅ CD, AB ≅ AC, and AD ≅ AD.

Using the Pythagorean Theorem where l is the length of the legs. ABC can be divided into two congruent triangles by drawing line segment AD, which is also the height of triangle ABC.

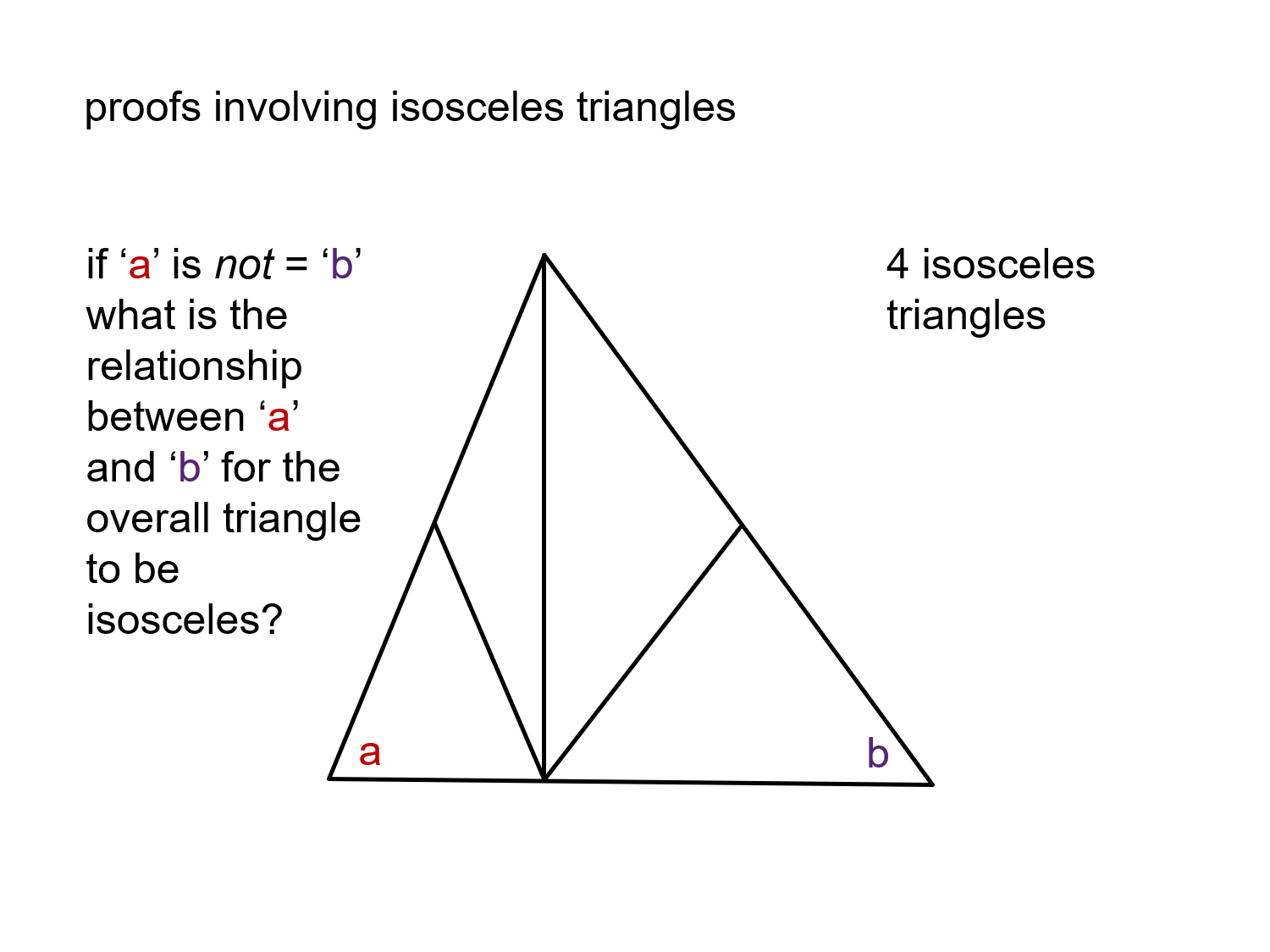
Refer to triangle ABC below.ĪB ≅ AC so triangle ABC is isosceles. The base angles of an isosceles triangle are the same in measure. The figure below shows these parts of an isosceles triangle. The altitude from the base of an isosceles triangle to its opposite vertex divides the triangle into two congruent right triangles.

Altitude - the perpendicular distance from the vertex of a triangle to the opposite side.

Base angle - the angles adjacent to the base of the isosceles triangle these are the two congruent angles.

Vertex angle - the angle opposite the base of the isosceles triangle.

Base - the third side of the triangle that is not congruent to the other two.

Legs - the congruent sides of the triangle.

The parts of an isosceles triangle are its legs, base, vertex angle, base angle, and altitudes. The yellow part of the pizza forms an isosceles triangle, as shown by the side and angle markings. A real life example of an isosceles triangle is a slice of pizza given that we exclude the curved part of the pizza crust, as shown in the figure below. What does an isosceles triangle look likeĪn isosceles triangle can look like various different things depending on the type of isosceles triangle.

To identify if a triangle is isosceles, check whether it has two congruent sides and angles if it does, it is isosceles if it doesn't, it is not isosceles. The isosceles triangle definition is a triangle that has two congruent sides and angles. The tally marks on the sides of the triangle indicate the congruence (or lack thereof) of the sides while the arcs indicate the congruence of the angles. The figure below shows an isosceles triangle example. Since the sides of a triangle correspond to its angles, this means that isosceles triangles also have two angles of equal measure. Home / geometry / triangle / isosceles triangle Isosceles triangleĪn isosceles triangle is a triangle that has at least two sides of equal length.